|
مقدمه :
 واژه
ی «سیاه چاله » اولین بار توسط فیزیکدان ها معرفی شد. این
واژه از دو قسمت سیاه و چاله تشکیل شده است. سیاه چاله به
جایگاهی در فضا گفته میشود که قابل رویت نیست (به عبارت
دیگر سیاه است.) ویژگی دیگر سیاه چاله این است که اجرام
سماوی را که به آن نزدیک می شوند، جذب می کند و در خود محو
می نماید. انسان هنوز قادر نیست محل دقیق این سیاه چاله ها
را مشخص کند اما می دانیم که جاهائی در فضا هستند که مانند
گرداب عمل می کنند و ستارگان و اجرام سماوی در یک مسیر مار
پیچ به این گرداب جذب می شوند. واژه
ی «سیاه چاله » اولین بار توسط فیزیکدان ها معرفی شد. این
واژه از دو قسمت سیاه و چاله تشکیل شده است. سیاه چاله به
جایگاهی در فضا گفته میشود که قابل رویت نیست (به عبارت
دیگر سیاه است.) ویژگی دیگر سیاه چاله این است که اجرام
سماوی را که به آن نزدیک می شوند، جذب می کند و در خود محو
می نماید. انسان هنوز قادر نیست محل دقیق این سیاه چاله ها
را مشخص کند اما می دانیم که جاهائی در فضا هستند که مانند
گرداب عمل می کنند و ستارگان و اجرام سماوی در یک مسیر مار
پیچ به این گرداب جذب می شوند.
مطالب بیشتر در باره ی سیاه چاله ها:
 به
طور مختصر، سیاه چاله قسمتی از فضاست که جرم بسیار زیادی
در آن متمرکز شده است و هیچ جرمی در مجاورت آن نمی تواند
از گرانش آن بگریزد. در حال حاضر بهترین نظریه در مورد
گرانش، نظریه ی نسبیت عام اینشتین است. ما نیز برای درک
بهتر جزئیات سیاه چاله ها باید به برخی نتایج نسبیت عام
رجوع کنیم. اما بیایید با تفکر در مورد گرانش در محیط های
عادی و در سطوح ساده شروع کنیم. به
طور مختصر، سیاه چاله قسمتی از فضاست که جرم بسیار زیادی
در آن متمرکز شده است و هیچ جرمی در مجاورت آن نمی تواند
از گرانش آن بگریزد. در حال حاضر بهترین نظریه در مورد
گرانش، نظریه ی نسبیت عام اینشتین است. ما نیز برای درک
بهتر جزئیات سیاه چاله ها باید به برخی نتایج نسبیت عام
رجوع کنیم. اما بیایید با تفکر در مورد گرانش در محیط های
عادی و در سطوح ساده شروع کنیم.
فرض کنید که بر روی سطح یک سیاره ایستادهاید و یک سنگی را
به بالا پرتاب می کنید. فرض کنید که آن را با قدرت زیاد
پرتاب نکرده اید. سنگ برای مدت کوتاهی به بالا حرکت می
کند، اما پس از مدتی شتاب گرانش سیاره آن را مجبور به سقوط
می کند. اگر شما سنگ را آن چنان پر قدرت پرتاب کنید که از
گرانش سیاره کاملا رها شود، برای همیشه به بالا رفتن خود
ادامه می دهد. سرعتی که شما نیاز دارید تا به سنگ بدهید و
از گرانش سیاره رهایش کنید سرعت گریز نامیده می شود. همان
طور که می دانید سرعت گریز سیاره به جرم آن بستگی دارد.
اگر سیاره چگال باشد، گرانش آن بسیار قوی خواهد بود، و
سرعت گریز بالا می رود. اما یک سیاره ی سبک تر سرعت گریز
کمی خواهد داشت. سرعت گریز همچنین به فاصله از مرکز سیاره
نیز بستگی دارد. هر چقدر که به مرکز سیاره نزدیکتر باشید
سرعت گریز شما بیشتر خواهد شد. سرعت گریز زمین 11.2
کیلومتر بر ثانیه است. در حالی که سرعت گریز ماه فقط 2.4
کیلومتر بر ثانیه است.
حال قسمتی از فضا را در نظر بگیرید که حاصل تمرکز عظیمی از
جرم با شعاع کم است که سرعت گریز آن بالاتر از سرعت نور
است. در حالی که هیچ چیز نمی تواند بالاتر از سرعت نور
حرکت کند، هیچ چیزی نمی تواند از گرانش آن بگریزد. حتی یک
باریکه ی نور نیز نخواهد توانست از گرانش آن بگریزد و به
سوی آن برمیگردد.
 ایده
ی چنین تمرکز جرمی که آنقدر چگال باشد که حتی نور در آن
گیر بیافتد مربوط به لاپلاس در قرن 18 می باشد. در حقیقت
بلافاصله بعد از اینکه اینشتین نسبیت عام خود را بسط داد
کارل شوارتز شیلد راه حلی ریاضی را که مربوط به معادله ی
نظریه ای که این جرم را توضیح می داد کشف کرد. کمی بعد
تلاش افرادی چون Oppenheimer، Volkoff و Synder در سال
1930 بود که باعث شد مردم جدی تر در مورد امکان وجود چنین
جرمی در عالم فکر کنند. این تحقیقات نشان می دهد که موقعی
که یک ستاره ی چگال سوخت خود را تمام می کند نمی تواند خود
را در مقابل گرانش خود حفظ کرده به یک سیاه چاله تبدیل می
شود. ایده
ی چنین تمرکز جرمی که آنقدر چگال باشد که حتی نور در آن
گیر بیافتد مربوط به لاپلاس در قرن 18 می باشد. در حقیقت
بلافاصله بعد از اینکه اینشتین نسبیت عام خود را بسط داد
کارل شوارتز شیلد راه حلی ریاضی را که مربوط به معادله ی
نظریه ای که این جرم را توضیح می داد کشف کرد. کمی بعد
تلاش افرادی چون Oppenheimer، Volkoff و Synder در سال
1930 بود که باعث شد مردم جدی تر در مورد امکان وجود چنین
جرمی در عالم فکر کنند. این تحقیقات نشان می دهد که موقعی
که یک ستاره ی چگال سوخت خود را تمام می کند نمی تواند خود
را در مقابل گرانش خود حفظ کرده به یک سیاه چاله تبدیل می
شود.
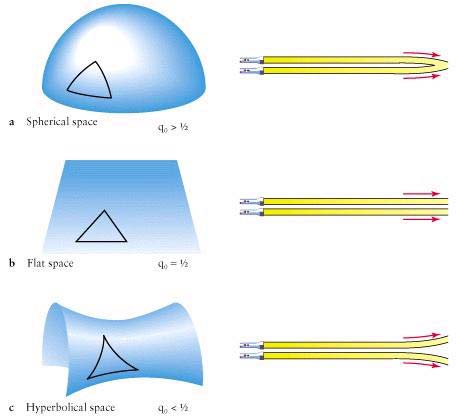
در نسبیت عام، گرانش باعث ایجاد خمیدگی در فضا – زمان می
شود. اجرام چگال باعث ایجاد خمیدگی در فضا و زمان می شوند.
بنابراین قوانین معمولی هندسه را در این موارد نمیتوان به
کار برد. در کنار یک سیاه چاله این خمیدگی فضا به مراتب
بیشتر است و همین باعث می شود که سیاه چاله خواص عجیبی
داشته باشد. یک سیاه چاله چیزی دارد که به خط افق اتفاق
(event horizon) مشهور است. این سطحی کروی شکلی است که مرز
سیاه چاله را تعیین می کند. شما می توانید وارد آن شوید
اما دیگر نمی توانید برگردید. به محض اینکه وارد افق شوید
محکوم به نزدیک شدن به مرکز سیاه چاله بدون هیچ توقفی
خواهید بود.
می توان گفت که خط افق جایی است که در آن سرعت گریز برابر
سرعت نور است. بیرون از افق سرعت گریز کمتر از سرعت نور
خواهد بود. پس اگر شما موشک های خود را به سختی به کار
بگیرید می توانید از آن رها شوید. اما اگر داخل افق باشید
هر چقدر هم که موشک های شما قوی باشند نمی توانید از آن
بگریزید.
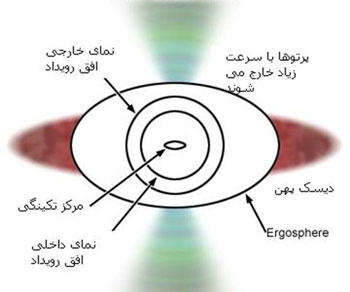
خط افق خواص هندسی عجیبی
دارد. برای مشاهده کننده ای که جایی دور از سیاه چاله
نشسته، خط افق مانند یک کره ی بسیار زیبا و ساکن و بدون
هیچ حرکتی جلوه می کند. اما هنگامی که به آن نزدیکتر می
شوید در می یابید که سرعت بسیار زیادی دارد. در حقیقت این
افق با سرعتی برابر سرعت نور به بیرون حرکت می کند. این
بیان می کند که چرا ورود به افق بسیار آسان است. اما خروج
از آن ممکن نیست. در حالی که افق با سرعت نور به خارج حرکت
می کند برای خارج شدن از آن باید با سرعتی بیشتر از سرعت
نور حرکت کرد. اما چون نمی توان بیش از سرعت نور حرکت کرد
پس نمی توان از آن خارج شد.
هنگامی که شما در افق هستید، فضا- زمان آنقدر منحرف می شود
تا جایی که مختصاتی که فاصله ی شعاعی شما را نشان می دهد
با زمان تغییر وظیفه می دهد. همان شعاع که نشان می دهد
چقدر از مرکز فاصله دارید مثل زمان کار خواهد کرد. یک
پیامد آن این است که شما نمی توانید از نزدیک شدن به مرکز
جلوگیری کنید. همانطور که در دنیای عادی نمی توانید جلوی
آمدن آینده ی خود را بگیرید. (با این تفاوت که در سیاه
چاله شعاع کمتر می شود یعنی فاصله ی شما از مرکز کمتر می
شود و در دنیای عادی زمان زیاد تر می شود.) در حقیقت شما
مجبورید که به مرکز یا شعاع صفر بروید. شاید سعی کنید که
با روشن کردن موشک های خود این کار را انجام بدهید اما این
کار نیز بی فایده است: به هر طرف که بدوید نمی توانید از
آمدن آینده ی خود جلوگیری کنید. تلاش برای برگشت بعد از
وارد شدن به افق مانند تلاش برای جلوگیری از آمدن روز بعد
خواهد بود.
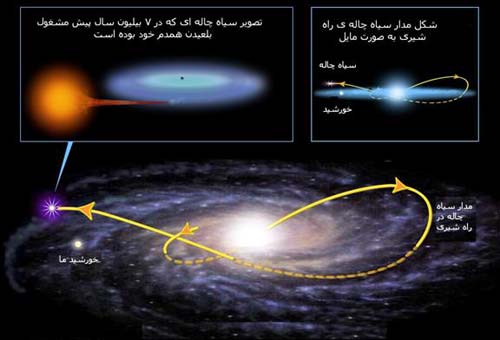
حرکت سیاهچاله در کهکشان راه شیری
سیاه
چاله های ریاضی:
در این جا سعی می کنیم
مجموعه هائی را مشخص کنیم که ویژگی گرداب ها یا سیاه چاله
های فضائی را دارند. به عبارت دیگر با تعریف فرایندهائی که
در حکم نوعی جاذبه هستند ، هر عدد طبیعی را به مجموعه ی
خاصی که سیاه چاله ی ریاضی می نامیم، هدایت کنیم.
قبل از بیان تعریف ، به چند مثال توجه کنید :
الف ـــ سیاه چاله ی زوج وفرد
مثال 1 ـــ عدد طبیعی زیر را در نظر بگیرید :
598721345069738
این عدد 15 رقم دارد ، 6 رقم آن زوج و 9 رقم آن فرد است.
با 15 و 6 و 9 عدد
زیر را می سازیم :
1569
این عدد 4 رقمی است ، 1 رقم زوج و 3رقم فرد دارد. با این
ارقام طبق همان
دستور عدد زیر ساخته میشود :
413
این عدد 3 رقمی است ، 1 رقم زوج و 2 رقم فرد دارد. با همان
فرایند عدد زیر حاصل میشود :
312
اگر فرایند مذکور را در باره ی این عدد به کار ببرید
،مجددا همین عدد را خواهید داشت.
مثال 2 ـــ اکنون عدد طبیعی زیر را در نظر می گیریم :
514131211109876543210
این عدد 21 رقمی است.تعداد ارقام زوج آن 8 و تعداد ارقام
فرد آن 13 است.
مطابق دستور العمل بالا به ترتیب خواهیم داشت:
21813
=> 523
=>
312
مثال 3ـــ عدد یک رقمی 8 نیز با همان فرایند به 312 می
رسد:
این عدد 1 رقمی ، دارای 1 رقم زوج بوده ورقم فرد ندارد.
8
=>
110
=>
312
اکنون این سئوال مطرح است
که اگر با هر عدد طبیعی شروع کنیم و فرایند بالا را به کار
ببریم به عدد
312 خواهیم رسید ؟
ضمن مثالهای قبل ملاحظه کردید که از هر عددی شروع کنیم،
به سرعت به یک عدد 3 رقمی می رسیم. بنا بر این کافی است
حالت های مختلف ارقام یک عدد سه رقمی را از نظر تعداد
ارقام زوج و فردبررسی کنیم. این حالت ها عبارتند از :
| |
تعداد ارقام
فرد |
تعداد ارقام
زوج |
عدد سه رقمی |
|
312
<=
330 |
0 |
3 |
3 |
|
312
<=
321 |
1 |
2 |
3 |
|
312 |
2 |
1 |
3 |
|
312
<=
303 |
3 |
0 |
3 |
بنا بر این فرایند مذکور سیاه چاله ی { 312 } =A را
معرفی می کند.
تابع متناظر با آن عبارت است از :
F ( n ) = abc
که در آن a تعداد ارقام عدد ،
b تعداد ارقام زوج
و c تعداد ارقام فرد آن است.
ب ـــ سیاه چاله ی حروف
:
مثال 1 ــ کلمه ی « گلپایگان » را در نظر بگیرید. تعداد
حروف آن 8 تا است. این عدد را به فارسی می نویسیم : « هشت
» این کلمه 3 حرف دارد. این عدد را نیز به فارسی می نویسیم
: « سه » کلمه ی اخیر دارای 2 حرف است. فارسی آن میشود : «
دو » این کلمه 2 حرف دارد. و از این به بعد روی عدد 2
متوقف می شویم. چرا؟
چند کلمه ی دیگر را با همین فرایند آزمایش می کنیم :

مثال 2 ـــ « آخاله »
=>
5 => «پنج »
=> 3
=> « سه »
=>2

مثال 3 ــ « مسجد جامع »
=>
8
=>
« هشت
»
=>
3
=>
«
سه »
=>
2

مثال 4ــ « هفده تن »
=>
6
=>
« شش »
=>
2

مثال 5 ـــ « سید السادات »
=>
10
=>
« ده
»
=>
2
مثال 6 ـــ « چو ایران نباشد تن من مباد »
=>
20
=>
«
بیست »
=>
4
=>
«چهار
»
=>
4
=>
«
چهار »
=>
..........
به نظر می رسد مجموعه ی { 2 ، 4 } =A یک سیاه چاله ی
حروف است.
در این جا نیز با هر کلمه یا عبارتی شروع کنیم ، به سرعت
به عددی یک رقمی می رسیم.
آیا با اعمال فرایند مذکور به اعداد 2 یا 4 می رسیم ؟
تمام اعداد یک رقمی را آزمایش می کنیم.:
یک
=>
2
=>
دو
=>
2
دو
=>
2
سه
=>
2
چهار
=>
4
=>
چهار
=>
4
پنج
=>
3
=>
سه
=>
2
شش
=>
2
هفت
=>
3
=>
سه
=>
2
هشت
=>
3
=>
سه
=>
2
نه
=>
2
اگر به جای حروف فارسی از حروف انگلیسی استفاده کنیم و
یا کلمه را به زبان آذری ، کردی ، و .... ادا کرده
و باحروف بنویسیم، به سیاه چاله
های دیگری می رسیم. |





